Reeksen en rijen in IQ tests

Een van de onderdelen die u vaak in IQ testen of assessments tegenkomt zijn cijfer reeksen. Vaak hebben deze reeksen de vorm van een aantal op elkaar volgende getallen, gevolgd door een ontbrekend getal dat u kunt kiezen uit een aantal antwoorden. Net zoals de meeste andere oefeningen in IQ testen hebben reeksen dus vaak een multiple choice vorm. Vaak zijn de berekeningen in een reeks relatief eenvoudig en het is daarom niet essentieel dat u heel snel moet kunnen rekenen om een cijferreeks goed te kunnen oplossen. Echter, om oplossingen ‘te proberen’ komt het wel goed van pas als u de basis beginselen van het rekenen zoals de tafels tot 10, delen, optellen en aftrekken van eenvoudige getallen, goed beheerst.
In een reeks bent u op zoek naar het patroon. Heeft u het patroon eenmaal gevonden, dan kunt u het ontbrekende getal meestal makkelijk uitrekenen. Soms is het patroon heel eenvoudig, maar het patroon kan ook heel lastig te vinden zijn. Reeksen en de onderliggende patronen kunnen heel verschillend zijn en het is daarom onmogelijk om op deze pagina een volledig overzicht van alle mogelijke patronen te geven. Wel staan op deze pagina een aantal varianties die vaak in IQ tests voorkomen en waarmee u kunt oefenen. Heeft u zelf een mooi voorbeeld? Geef het dan door aan de redactie via de contactpagina. Vaak bevatten reeksen alleen hele getallen (integers), maar reeksen kunnen ook breuken, letters of zelfs symbolen bevatten.
Er bestaat geen vaste methode waarmee u in alle gevallen het juiste antwoord kunt vinden. De voorbeelden en hulpmiddelen op deze pagina’s helpen u om een aantal veelgebruikte patronen te herkennen, maar zullen niet in alle opgaven werken.
hulpmiddel 1: het eerste verschil
Een veelgebruikte methode is om de verschillen tussen de opeenvolgende getallen te bepalen, en aan de hand van het patroon in die verschillen te bepalen wat het ontbrekende getal moet zijn. Een voorbeeld daarvan:
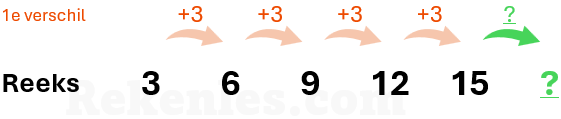
In bovenstaand voorbeeld is het verschil tussen de opvolgende getallen telkens het getal 3. Het goede antwoord in dit geval is 18 (namelijk 15 + 3).
hulpmiddel 2: het tweede verschil
Hierin kijkt u naar het verschil van het verschil. De getallen in de reeks in het onderstaande voorbeeld lijken op het eerste gezicht geen enkel verband met elkaar te hebben. Maar als je kijkt naar de tweede verschilreeks, zie je dat de getallen eigenlijk een hele logische volgorde hebben:
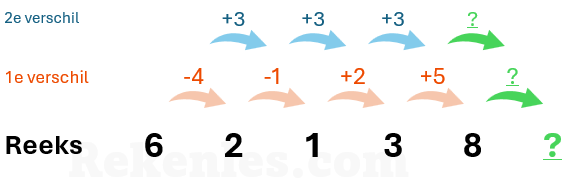
In bovenstaand voorbeeld neemt het verschil telkens toe met 3. De laatste optelling was +5, dus de eerstvolgende optelling wordt +8. Het goede antwoord in dit geval is 16 (namelijk 8 + 8).
hulpmiddel 3: snel kunnen (hoofd)rekenen
Hoewel snel kunnen rekenen niet automatisch betekent dat u alle soorten reeksen zult oplossen, kan bijvoorbeeld het snel kunnen herkennen van breuken of vermenigvuldigingen ernorm helpen om snel tot het juiste antwoord te komen.
hulpmiddel 4: herken specifieke reeksen
Soms is een reeks eenvoudig te herkennen omdat het simpelweg een in de wiskunde bekende rij getallen is. Voorbeelden hiervan zijn bijvoorbeeld de reeks met Fibonacci getallen of een reeks die uit priemgetallen bestaat. Specifieke reeksen die op deze pagina worden behandeld:
- Lineaire reeks oplopend
- Lineaire reeks aflopend
- Toenemend of afnemend verschil
- Afwisselende bewerking
- Om en om
- Reeks met breuken
- De Fibonacci reeks
- Reeks met kwadraten
- Priemgetallen
Lineair oplopend
Dit is waarschijnlijk de makkelijkste variant en deze zult u daarom vaak eenvoudig herkennen:
2, 4, 6, 8, 10, ...
Een iets ingewikkeldere variant op de lineaire reeks is de variant die begint met een of meer negatieve getallen. In onderstaand voorbeeld wordt in iedere stap 3 opgesteld, alleen begint de reeks bij het getal -5.:
-5, -2, 1, 4, 7, 10, ...
Lineair aflopend
De lineaire reeks kan natuurlijk ook aflopend zijn:
10, 6, 2, -2, ...
In bovenstaande voorbeelden werd de reeks gemaakt door steeds hetzelfde getal bij het vorige getal op te tellen of af te trekken. Dat hoeft niet altijd zo te zijn: ook met eenvoudige vermenigvuldigingen of delingen kan een reeks worden gemaakt.
Toenemend of afnemend verschil
Een voorbeeld van een oplopende verschilreeks is: 2, 4, 8, 14, 22. U ziet dat de verschillen tussen de getallen steeds groter worden. Wanneer je de eerste verschilreeks uitschrijft zie je dat die bestaat uit de getallen 2, 4, 6, en 8. Je ziet dat het verschil steeds groter wordt, namelijk met 2 met iedere stap. De tweede verschilreeks is hier dus +2. Het juiste antwoord voor deze reeks is dus 32; in de laatste stap wordt het getal 10 opgeteld.
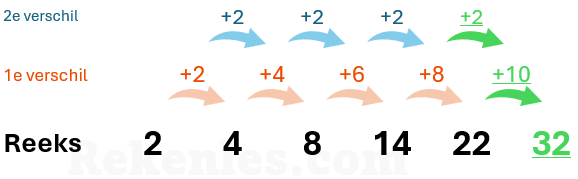
De reeks kan er een ingewikkelder uitzien als in de reeks negatieve getallen voorkomen, zoals bijvoorbeeld in de reeks -8, -4, 4, 16. Deze reeks is echter niet zo ingewikkeld als hij eruit ziet: ook hier komt u redelijk eenvoudig tot de oplossing door de tweede verschil reeks uit te schrijven:
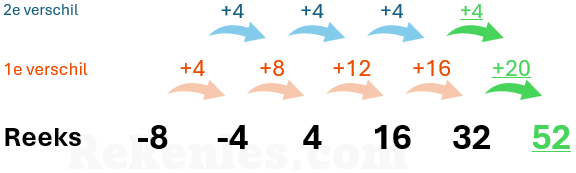
Bovenstaande variant is het verschil telkens positief (het opvolgende getal is groter dan het vorige getal). De reeks kan natuurlijk ook negatief zijn. Een voorbeeld van een negatieve reeks is:
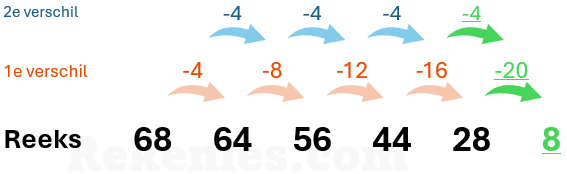
De ingewikkeldste variant van de tweede verschilreeks is waar de bewerking van de eerste verschilreeks van positief naar negatief gaat, of van negatief naar positief. Dit is bijvoorbeeld het geval in de reeks 50, 62, 65, 59, 44.
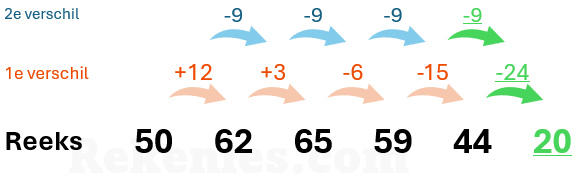
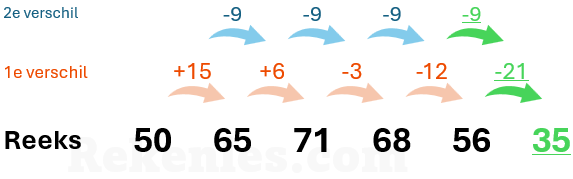
Het verschil hier is aan het begin positief, maar wordt met iedere stap 9 kleiner. Uiteindelijk wordt het verschil daarom negatief waardoor de eerste verschilrij negatief wordt. Anderskom, van negatief naar positief kan natuurlijk ook. Dat is bijvoorbeeld het geval in de reeks 50, 65, 71, 68, 56.
Afwisselende bewerking
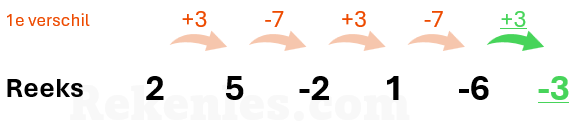
De bewerkingen tussen de getallen hoeft niet telkens hetzelfde te zijn, maar kunnen elkaar ook opvolgend afwisselen. In de reeks 2, 5, -2, 1, -6, wisselen de bewerking +3 en -7 elkaar af:
Om en om
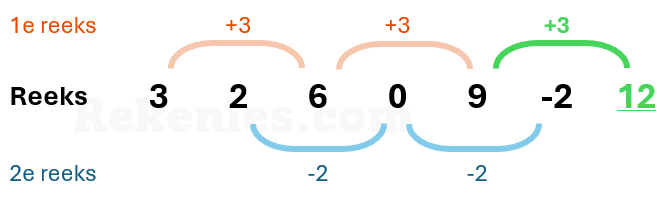
Bij dit type reeks bestaat de reeks eigenlijk uit twee afzonderlijke reeksen. In de reeks 3, 2, 6, 0, 9, -2 uit het volgende voorbeeld bestaat de ene reeks uit de bewerking +3, en de andere reeks uit de bewerking -2: Het antwoord is 9, namelijk: bij iedere stap in de eerste reeks wordt het getal 2 opgeteld (1, 3, 5, 7). In de tweede reeks wordt het getal telkens met 2 vermenigvuldigd (2, 4, 8, 16)
Reeks met breuken
Breuken zorgen vaak voor verwarring in cijferreeksen. Staan er breuken in een reeks, dan kan het helpen om de reeks te vereenvoudigen tot gehele getallen. Daarnaast worden in sommige tests de antwoorden gegeven zonder dat deze zijn vereenvoudigd: als het goede antwoord is 4, zou dat bijvoorbeeld in een breuk gegeven kunnen worden als 8/2.
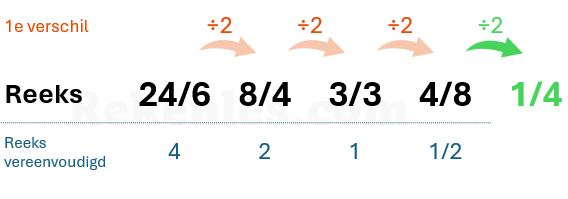
Daarnaast helpt het om goed te kunnen rekenen met breuken en om de tafels te beheersen. Let op: in sommige gevallen zal het antwoord ook als breuk gegeven zijn. In het bovenstaande voorbeeld zou het antwoord bijvoorbeeld kunnen zijn 4/16 of 3/12.
Fibonacci reeks
Een andere reeks die vaak voorkomt is de Fibonacci reeks of een variatie daarop. De meest eenvoudige vorm is de originele Fibonacci reeks die de vorm heeft 1, 1, 2, 3, 5, 8, 13, 21, ...
Het grappige aan de Fibonacci reeks is dat de eerste verschilreeks de reeks zelf is! Kijk maar:
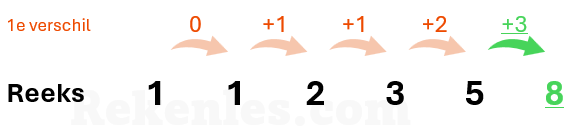
In de Fibonacci reeks worden telkens de laatste twee getallen van de reeks bij elkaar opgeteld om tot het volgende getal te komen. In het voorbeeld is het volgende getal dus 21 (8 + 13).
De Fibonacci reeks hoeft niet te beginnen met het getal 1, maar kan ook met een ander getal beginnen: 13, 21, 44, 65, 109. Het juiste antwoord is hier 174 (65 + 109).
Daarnaast is er een groot aantal varianten op de Fibonacci reeks waarbij de methodiek van de twee voorgaande getallen bij elkaar optellen hetzelfde is, maar de getallen niet de Fibonacci reeks zelf zijn. Bijvoorbeeld: 2, 2, 4, 6, 10, 16, 26, .... In dit voorbeeld is het volgende getal 42, namelijk 16 plus 26.
Priemgetallen
De priemgetallen komt men als reeks ook wel eens tegen. Een korte reminder: een priemgetal is een getal dat alleen deelbaar is door het getal zelf en door het getal 1. Als u hierover meer wilt weten kijk dan op de speciale pagina over priemgetallen.
2, 3, 5, 7, 11, ...
Het volgende priemgetal in de reeks is het getal 13. Uiteraard kan de reeks ook met een ander priemgetal beginnen, bijvoorbeeld:
41, 43, 47, 53, 59, ...
Het volgende getal in de reeks is het priemgetal 61. Er is geen efficiënte manier om de priemgetallen te leren, maar wat wel helpt is als u de tafels goed beheerst; u zult dan sneller herkennen dat de priemgetallen niet als antwoord op de tafels voorkomen.
Kwadraat
Met kwadraten kan ook een reeks worden gemaakt. Als u de tafels enigszins beheerst zult u deze reeks snel herkennen:
4, 9, 16, 25, 36, ...
Het antwoord is 49, namelijk 7 x 7. De reeks kan ook met een hoger getal beginnen:
81, 100, 121, 144, ...
Het antwoord hier is 169, namelijk 13 x 13.
Een reeks die uit kwadraten bestaat kunt u ook zichtbaar maken met een tweede verschilreeks:
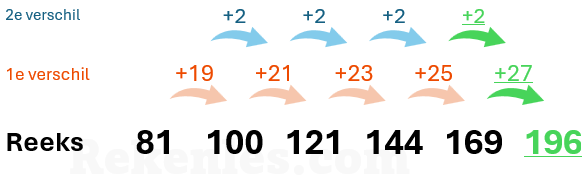
Rekenles.com 2024 ©

