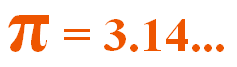
Veel mensen kennen het symbool waarmee het getal Pi wordt afgebeeld. Op deze pagina leggen we uit wat Pi precies is en waarvoor het wordt gebruikt.
Een getal dat een verhouding aangeeft
Pi is niets meer dan een getal dat ongeveer 3,14 groot is. Pi is een irrationeel getal, dat betekent dat je Pi niet kunt schrijven als een breuk van twee gehele getallen. Met irrationele getallen is iets bijzonders aan de hand: na de komma volgt een oneindig aantal getallen, waarin geen enkele volgorde of regelmaat zit.
Pi heeft alles te maken met cirkels. Voordat we daar meer over vertellen is het goed om drie dingen van een cirkel te weten: de straal is de afstand tussen het middelpunt van een cirkel en de rand van de cirkel. De diameter is de afstand van de ene kant van de cirkel naar de andere kant. De diameter is dus precies twee keer zo groot als de straal van de cirkel. De omtrek is de lengte van de lijn die je trekt als je de cirkel precies een keer rond gaat.
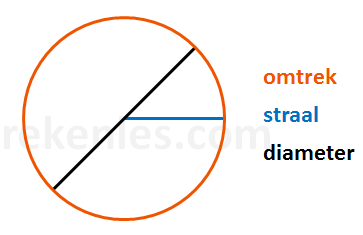
Pi is de verhouding tussen de lengte van de diameter van een cirkel en de lengte van de omtrek van dezelfde cirkel. De omtrek van de cirkel is namelijk precies Pi maal de diameter. Stel je het volgende voor: een cirkel heeft een diameter van 1 meter. De omtrek van de cirkel is dan precies 1 x Pi = 1 x 3,1415 = 3,1415 meter. Als de diameter van de cirkel 3 meter is, dan is de omtrek dus 3 x Pi = 3 x 3,1415 = 9,4245 meter.
Omtrek en de oppervlakte van een cirkel
De bekendste formules waarin het getal Pi voorkomt zijn de formules om de omtrek en de oppervlakte van een cirkel te berekenen. Zoals we gezien hebben bereken je de omtrek van de cirkel met de formule 2 x Pi x r. De oppervlakte van de cirkel bereken je met de formule 2 x Pi x r x r, of 2 x Pi x r^2. Zie de afbeelding hieronder:
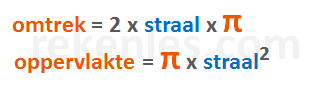
Voorbeeld: omtrek van een cirkel met straal (r) van 5
Formule omtrek: 2 x Pi x r
Invullen met Pi en r=5: 2 x 3,1415 x 5 = 31,415
Omtrek = 31,415
Let op: het getal Pi is in werkelijkheid oneindig lang. De omtrek van deze cirkel is dus ongeveer 31,415 , en niet precies 31,415!
Voorbeeld: oppervlakte van een cirkel met straal (r) van 5
Formule oppervlakte: 2 x Pi x r^2
Invullen met Pi en r=5: 2 x 3,1415 x 5^2 (5^2 is vijf tot de tweede macht, oftewel 5 x 5)
Oppervlakte = 157,057
Pi en Tau
Als je over Pi spreekt kom je soms nog een ander getal tegen, het getal Tau. Tau is simpel: het is precies twee keer Pi! Wetenschappers hebben sinds de jaren '80 onderzoek gedaan naar het gebruik van het getal Pi, en kwamen tot de conclusie dat je makkelijker kunt rekenen en mooiere formules krijgt als je Tau gebruikt in plaats van Pi: als je Tau gebruikt, wordt de formule voor de omtrek van een cirkel dus straal x Tau.
Rekenles.com 2024 ©

